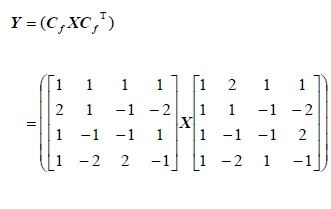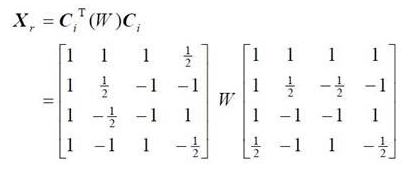本文主要记录 X264 中对于 DCT 变换的初始化过程。宏块的编码过程就是一个DCT变换+量化的过程。
DCT 变换的核心理念就是把图像的低频信息(对应大面积平坦区域)变换到系数矩阵的左上角,而把高频信息变换到系数矩阵的
右下角,之后在压缩时就可以去除掉人眼不敏感的高频信息(位于矩阵右下角的系数),从而达到压缩数据的目的。
关于 DCT 的计算,都是通过x264_dct_init函数内定义的DCT和IDCT函数完成的,定义如下:
1
2
3
4
5
6
7
8
9
10
11
12
| void x264_dct_init(int cpu, x264_dct_function_t *dctf)
{
dctf->sub4x4_dct = sub4x4_dct;
dctf->add4x4_idct = add4x4_idct;
dctf->sub8x8_dct = sub8x8_dct;
dctf->sub8x8_dct_dc = sub8x8_dct_dc;
dctf->add8x8_dct = add8x8_dct;
dctf->add8x8_dct_dc = add8x8_dct_dc;
...
}
|
DCT 变化理论比较抽象,先从 X264 中代码入手,然后经过 DCT 变换后,比较变换前和变换后的数据,能够更好的理解 DCT 变换。
X264 中对 DCT 各类函数的定义都在common/dct.c里面。其中 sub4x4_dct 定义如下:
sub4x4_dct
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| static inline void pixel_sub_wxh( dctcoef *diff, int i_size,
pixel *pix1, int i_pix1, pixel *pix2, int i_pix2 )
{
for( int y = 0; y < i_size; y++ )
{
for( int x = 0; x < i_size; x++ )
diff[x + y*i_size] = pix1[x] - pix2[x];
pix1 += i_pix1;
pix2 += i_pix2;
}
}
static void sub4x4_dct( dctcoef dct[16], pixel *pix1, pixel *pix2 )
{
dctcoef d[16];
dctcoef tmp[16];
pixel_sub_wxh( d, 4, pix1, FENC_STRIDE, pix2, FDEC_STRIDE );
for( int i = 0; i < 4; i++ )
{
int s03 = d[i*4+0] + d[i*4+3];
int s12 = d[i*4+1] + d[i*4+2];
int d03 = d[i*4+0] - d[i*4+3];
int d12 = d[i*4+1] - d[i*4+2];
tmp[0*4+i] = s03 + s12;
tmp[1*4+i] = 2*d03 + d12;
tmp[2*4+i] = s03 - s12;
tmp[3*4+i] = d03 - 2*d12;
}
for( int i = 0; i < 4; i++ )
{
int s03 = tmp[i*4+0] + tmp[i*4+3];
int s12 = tmp[i*4+1] + tmp[i*4+2];
int d03 = tmp[i*4+0] - tmp[i*4+3];
int d12 = tmp[i*4+1] - tmp[i*4+2];
dct[i*4+0] = s03 + s12;
dct[i*4+1] = 2*d03 + d12;
dct[i*4+2] = s03 - s12;
dct[i*4+3] = d03 - 2*d12;
}
}
|
上面的代码实现的是下面矩阵乘法:
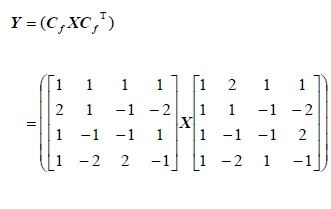
4x4 DCT 反变换实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| static ALWAYS_INLINE pixel x264_clip_pixel(int x)
{
return ((x & ~PIXEL_MAX)?(-x)>>31 & PIXEL_MAX:x);
}
static void add4x4_idct(pixel *p_dst, dctcoef dct[16])
{
dctcoef d[16];
dctcoef tmp[16];
for(int i = 0; i < 4; i++)
{
int s02 = dct[0*4+i] + dct[2*4+i];
int d02 = dct[0*4+i] - dct[2*4+i];
int s13 = dct[1*4+i] + (dct[3*4+i]>>1);
int d13 = (dct[1*4+i]>>1) - dct[3*4+i];
}
for(int i = 0; i < 4; i++)
{
int s02 = tmp[0*4+i] + tmp[2*4+i];
int d02 = tmp[0*4+i] - tmp[2*4+i];
int s13 = tmp[1*4+i] + (tmp[3*4+i]>>1);
int d13 = (tmp[1*4+i]>>1) - tmp[3*4+i];
d[0*4+i] = (s02 + s13 + 32) >> 6;
d[1*4+i] = (d02 + d13 + 32) >> 6;
d[2*4+i] = (d02 - d13 + 32) >> 6;
d[3*4+i] = (s02 - d13 + 32) >> 6;
}
for(int y = 0; y < 4; y++)
{
for(int x = 0; x < 4; x++)
p_dst[x] = x264_clip_pixel(p_dst[x] + d[y*4+x]);
p_dst += FDEC_STRIDE;
}
}
|
上面的代码实现的是下面矩阵乘法:
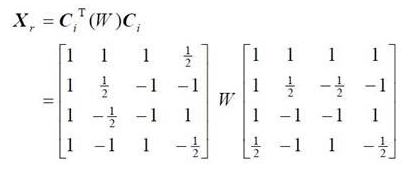
其中的pixel_sub_wxh是获取 pix1 和 pix2 两块数据的残差。这里对 pix1 和 pix2 随意举两个相似的4x4的矩阵作为例子,
之所以要随意是为了突出其普遍性,适用于大多数的 DCT 变换;而相似是因为 pix1 为编码块,pix2 为预测块,它们理论上就应该是相似的。为此举例如下:
$pix1[4x4]=[(23,24,27,29),(24,25,28,28),(26,28,29,29),(26,25,28,30)];$
$pix2[4x4]=[(20,23,27,29),(23,24,26,27),(25,26,25,28),(26,24,28,30)];$
将 pix1 和 pix2 经过pixel_sub_wxh的计算后,得到矩阵d[4x4]为[(3,1,0,0),(1,1,2,1),(1,2,4,1),(0,1,0,0)]。
经第一个for循环后得到tmp[4x4]=[]