前面两篇分别介绍了如何使用 NEON 来加载和存储数据,如何使用 NEON 处理多余的数据。这一篇介绍一点儿使用的数据处理——矩阵相乘。
矩阵
本篇文章会分析如何有效的完成4x4矩阵相乘,这种操作在 3D 图形中经常会用到。假设矩阵存放到内存中,并且是列优先的顺序,该格式在 OpenGL-ES 中使用。
算法(Algorithm)
先详细的检测一下矩阵相乘的操作,通过把计算扩展开,并确定哪些子操作可以使用 NEON 指令实现。
在上图中,我们将第一个矩阵的每一列(红色标记)乘以在第二个矩阵中对应的数值(蓝色标记),然后将结果加起来,得到结果中的一个列的数值。这个操作将被重复四次。
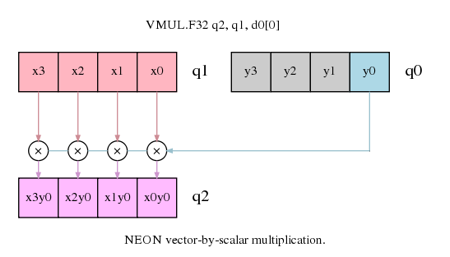
如果每个列都是在 NEON 寄存器中的一个向量,我们能够用 vector-by-scalar multiplication 指令来计算每个列。即上图中显示的指令。我们可以用同样指令的累计版本来将结果都加起来组成每一列的结果。
当我们处理第一个矩阵的列,产生结果中的一列时,读取和写入数据到或者从内存中都是一个线性操作,不需要交错读取及存储指令。
代码
浮点数运算
首先,我们先关注乘以单精度浮点数矩阵的实现。
从内存中加载矩阵到 NEON 寄存器,该矩阵是使用列顺序进行存储,所以存储的列都是线性的存储在内存中。一个列能够用 VLD1 指令加载到 NEON 寄存器,用 VST1 写入到内存。
1
2
3
4
vld1.32 { d16-d19 } , [ r1 ]! @ load first eight elements of matrix 0
vld1.32 { d20-d23 } , [ r1 ]! @ load second eight elements of matrix 0
vld1.32 { d0-d3 } , [ r2 ]! @ load first eight elements of matrix 1
vld1.32 { d4-d7 } , [ r2 ]! @ load second eight elements of matrix 1
NEON 有 32 个 64 位寄存器,我们可以从矩阵中加载所有的数据到寄存器,并且还有剩余的寄存器可以用来作为累加用。这里 d16 到 d23 保存第一个矩阵中的 16 个数据,而 d0 到 d7 保存第二个矩阵中的 16 个数据。
D and Q 寄存器
大部分 NEON 指令能够用一下两种方式使用寄存器组:
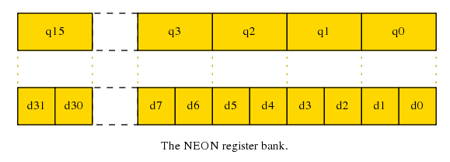
32 个双字寄存器, 64bits 大小,从 d0 到 d31。
16 个四字寄存器, 128bits 大小,从 q0 到 q15。
这些寄存器用别名表示,因此,在 Q 寄存器,以及在相对应的两个 D 寄存器中,数据都是一样的。例如,q0 可被分为 d0 及 d1,数据可以在两种模式下进行访问。在 C 中,这种方式类似于 union。
对于浮点数矩阵乘法的例子,我们频繁的使用 Q 寄存器,因为我们处理 4 个 32-bit 浮点数的列,这将对应于一个 128 位的 Q 寄存器。
回到代码中
应用 NEON 乘法指令,我们能够计算矩阵相乘的一个列。
1
2
3
4
vmul.f32 q12 , q8 , d0 [ 0 ] @ multiply col element 0 by matrix col 0
vmla.f32 q12 , q9 , d0 [ 1 ] @ multiply-acc col element 1 by matrix col 1
vmla.f32 q12 , q10 , d1 [ 0 ] @ multiply-acc col element 2 by matrix col 2
vmla.f32 q12 , q11 , d1 [ 1 ] @ multiply-acc col element 2 by matrix col 3
第一个指令实现了在矩阵乘法分解图中的操作,x0、x1、x2 和 x3(在 q8 寄存器中)分别乘以 y0(d0 的第 0 个数据),结果保存在 q12。接下来的指令用于处理第一个矩阵中的其他列,乘以第二个矩阵第一列中对应的元素。结果将会累加到 q12,来构成最终结果的第一列。
需要注意的是,乘法指令中的标量是 D 寄存器,尽管q0[3]的数据与d1[1]相同,但是这里使用d1[1]更加说得过去,并且 GNU 汇编器并不支持这种格式。因此,我们不得不使用 D 寄存器。
宏:
1
2
3
4
5
6
.macro mul_col_f32 res_q , col0_d , col1_d
vmul.f32 \ res_q , q8 , \ col0_d [ 0 ] @ multiply col element 0 by matrix col 0
vmla.f32 \ res_q , q9 , \ col0_d [ 1 ] @ multiply-acc col element 1 by matrix col 1
vmla.f32 \ res_q , q10 , \ col1_d [ 0 ] @ multiply-acc col element 2 by matrix col 2
vmla.f32 \ res_q , q11 , \ col1_d [ 1 ] @ multiply-acc col element 3 by matrix col 3
.endm
4x4 浮点矩阵相乘可以被这样实现:
1
2
3
4
5
6
7
8
9
10
11
12
vld1.32 { d16-d19 } , [ r1 ]! @ load first eight elements of matrix 0
vld1.32 { d20-d23 } , [ r1 ]! @ load second eight elements of matrix 0
vld1.32 { d0-d3 } , [ r2 ]! @ load first eight elements of matrix 1
vld1.32 { d4-d7 } , [ r2 ]! @ load second eight elements of matrix 1
mul_col_f32 q12 , d0 , d1 @ matrix 0 * matrix 1 col 0
mul_col_f32 q13 , d2 , d3 @ matrix 0 * matrix 1 col 1
mul_col_f32 q14 , d4 , d5 @ matrix 0 * matrix 1 col 2
mul_col_f32 q15 , d6 , d7 @ matrix 0 * matrix 1 col 3
vst1.32 { d24-d27 } , [ r0 ]! @ store first eight elements of result
vst1.32 { d28-d31 } , [ r0 ]! @ store second eight elements of result
定点运算
使用定点数运算通常比浮点数更快,因为它占用更小的内存带来读取及写入数值,并且整数的乘法通常来说更快。然而,在使用定点数运算时,当需要保证程序要求的计算精度时,你必须仔细选择表示方法来避免溢出或者饱和。
使用定点数进行矩阵乘法与浮点数非常类似。在这个例子中个,我们使用 Q1.14 定点数格式,但是操作上与其他格式类似,可能只需要最终左移的位数。
宏定义:
1
2
3
4
5
6
7
8
.macro mul_col_s16 res_d , col_d
vmull.s16 q12 , d16 , \ col_d [ 0 ] @ multiply col element 0 by matrix col 0
vmlal.s16 q12 , d17 , \ col_d [ 1 ] @ multiply-acc col element 1 by matrix col 1
vmlal.s16 q12 , d18 , \ col_d [ 2 ] @ multiply-acc col element 2 by matrix col 2
vmlal.s16 q12 , d19 , \ col_d [ 3 ] @ multiply-acc col element 3 by matrix col 3
vqrshrn.s32 \ res_d , q12 , #14 @ shift right and narrow accumulator into
@ Q1.14 fixed point format , with saturation
.endm
与浮点数版本的宏进行对比,你将会发现:
数值是16位而不是32为,我们可以使用D寄存器保存4个输入。
两个16位数的相乘结果是一个32位数,我们使用VMULL及VMLAL,因为它们将保存结果至Q寄存器,使用两倍于数据的大小来保存所有的位数。
最后的结果为16位,但是累加器是32位的。我们通过VQRSHRN获取16位结果,一个向量,饱和计算,四舍五入,右移窄运算。这将把所有正确的值加起来到各自的数据,右移并饱和计算到新的更窄的数据大小。
32位数到16位数的减少对内存访问有所影响。数据会被加载和存储使用更少的指令,代码如下:
1
2
3
4
5
6
7
8
9
vld1.16 { d16-d19 } , [ r1 ] @ load sixteen elements of matrix 0
vld1.16 { d0-d3 } , [ r2 ] @ load sixteen elements of matrix 1
mul_col_s16 d4 , d0 @ matrix 0 * matrix 1 col 0
mul_col_s16 d5 , d1 @ matrix 0 * matrix 1 col 1
mul_col_s16 d6 , d2 @ matrix 0 * matrix 1 col 2
mul_col_s16 d7 , d3 @ matrix 0 * matrix 1 col 3
vst1.16 { d4-d7 } , [ r0 ] @ store sixteen elements of result
如果考虑到调度的话
我们会在以后的文章中讨论调度的细节,现在的话,可以看看在代码中查看改进指令调度的影响。
在宏中,临近的乘法指令写入到相同的寄存器,使得NEON流水线在开始下个指令执行时必须等待每个乘法完成。
如果我们把这些指令移出宏然后重新安排顺序,我们能够分离出那些依赖于其他指令的部分,这部分指令能够在其他指令在后台完成时也被执行。
在这个实例中,我们重组代码来分离累加寄存器的使用。
1
2
3
4
5
6
7
8
9
vmul.f32 q12 , q8 , d0 [ 0 ] @ rslt col0 = ( mat0 col0 ) * ( mat1 col0 elt0 )
vmul.f32 q13 , q8 , d2 [ 0 ] @ rslt col1 = ( mat0 col0 ) * ( mat1 col1 elt0 )
vmul.f32 q14 , q8 , d4 [ 0 ] @ rslt col2 = ( mat0 col0 ) * ( mat1 col2 elt0 )
vmul.f32 q15 , q8 , d6 [ 0 ] @ rslt col3 = ( mat0 col0 ) * ( mat1 col3 elt0 )
vmla.f32 q12 , q9 , d0 [ 1 ] @ rslt col0 += ( mat0 col1 ) * ( mat1 col0 elt1 )
vmla.f32 q13 , q9 , d2 [ 1 ] @ rslt col1 += ( mat0 col1 ) * ( mat1 col1 elt1 )
...
...